قضیه بیز (به انگلیسی: Bayes’ theorem) روشی برای دسته بندی پدیده‌ها، بر پایه احتمال وقوع یا عدم وقوع یک پدیده‌است و در نظریه احتمالات با اهمیت و پرکاربرد است. اگر برای فضای نمونه‌ای مفروضی بتوانیم چنان افرازی انتخاب کنیم که با دانستن اینکه کدامیک از پیشامدهای افراز شده رخ داده‌است، بخش مهمی از عدم‌اطمینان تقلیل می یابد.
این قضیه از آن جهت مفید است که می‌توان از طریق آن احتمال یک پیشامد را با مشروط کردن نسبت به وقوع و یا عدم وقوع یک پیشامد دیگر محاسبه کرد. در بسیاری از حالت‌ها، محاسبهٔ احتمال یک پیشامد به صورت مستقیم کاری دشوار است. با استفاده از این قضیه و مشروط کردن پیشامد مورد نظر نسبت به پیشامد دیگر، می‌توان احتمال مورد نظر را محاسبه کرد.
این رابطه به خاطر بزرگداشت توماس بیز فیلسوف انگلیسی به نام فرمول بیز معروف است.
محتویات
- ۱ معادله اصلی
- ۲ برهان
- ۳ یادگیری ماشینی به کمک نظریه بیز
- ۳.۱ تئوری بیز در یادگیری ماشین
- ۳.۲ تعریف مفاهیم اولیه
- ۳.۳ روشهای یادگیری بیزی ماشینی
- ۴ مثال
- ۵ جستارهای وابسته
- ۶ منابع
معادله اصلی
فرض می‌کنیم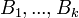 
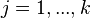
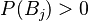
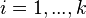
یک افراز برای فضای نمونه‌ای 
تشکیل دهند. طوری که به ازای هر 
، داشته باشیم 
و فرض کنید 
پیشامدی با فرض 
باشد، در اینصورت به ازای 
، داریم:
برهان
طبق تعریف احتمال شرطی داریم 
. صورت کسر قضیه طبق دستور حاصلضرب در احتمال شرطی، برابر با 
و مخرج کسر بنابر قضیه قانون احتمال کل، برابر 
است.
اگر A و B دو پیشامد مفروض باشند، می‌توان پیشامد A را به صورت زیر در نظر بگیریم:
A=AB∪AB’
زیرا نقطه‌ای که در A باشد باید یا در هر دوی A و B باشد و یا این که در A باشد و در B وجود نداشته باشد.از طرفی می دانیم AB و AB’ ناسازگار هستند، پس می‌توان نوشت:
P(A)=P(AB)+P(AB’)=P(A│B)P(B)+P(A│B^c )P(B’ )=p(A│B)P(B)+P(A│B’)1-P(B)
این رابطه بیان می‌دارد که احتمال به وقوع پیوستن پیشامد A یک میانگین وزنی از احتمال شرطی (A│B) و احتمال شرطی (A│B’) می‌باشد. وزن داده شده به هر احتمال شرطی به اندازهٔ احتمالی است که A نسبت به آن مشروط شده‌است.رابطه بالا را می‌توان به صورت زیر تعمیم داد. فرض کنید پیشامدهای B1، B2، … و Bn پیشامدهای دو به دو ناسازگار باشند از طرفی رابطهٔ زیر نیز بین این پیشامدها برقرار است:
U(i=1)^n Fi=S
از این عبارت این گونه می‌توان استنباط کرد که حتماً یکی از پیشامدهای B1، B2، … و Bn باید اتفاق بیفتداز طرفی می دانیم که پیشامدهای AB_iکه (i=1,2،…,n) دو به دو ناسازگار هستند و می‌نویسیم
A=⋃_(i=1)^n AB_i
از این جا می‌توان نوشت:
این رابطه بیان می‌دارد که چگونه می‌توان (P(A را با مشروط کردن به یکی از پیشامدهای داده شدهٔ B1، B2، … و Bn محاسبه نمود. به طور کلی این رابطه باین می‌دارد که P(A) برابر است با میانگین وزنی (P(A│B_c به نحوی که هر وزن هر جمله برابر با احتمالی است که به آن مشروط گردیده‌است حال فرض کنید که پیشامد A اتفاق افتاده و می‌خواهیم احتمال این که یکی از پیشامدهای Bi اتفاق افتاده باشد را حساب کنیم:
یادگیری ماشینی به کمک نظریه بیز
برای نگرش بیزی به یادگیری ماشین (و یا هر فرایند دیگر) می‌باید نخست:
- دانش موجود در باره موضوع را بصورت احتمالاتی فرموله کنیم:برای اینکار باید مقادیر کیفی دانش را بصورت توزیع احتمال، فرضیات استقلال و غیره مدل کرد. این مدل دارای پارامترهای ناشناخته‌ای خواهد بود که برای هر یک از مقادیر ناشناخته، توزیع احتمال اولیه‌ای در نظر گرفته می‌شود که بازگو کننده باور ما به محتمل بودن هر یک ازاین مقادیر بدون دیدن داده‌است.
- با جمع آوری داده و مشاهدهٔ آن، مقدار توزیع احتمال ثانویه را محاسبه می‌کنیم
- با استفاده از این احتمال ثانویه:
- به یک نتیجه گیری در مورد عدم قطعیت می‌رسیم
- با میانگین گیری روی مقادیر احتمال ثانویه پیش بینی انجام می‌دهیم
- برای کاهش خطای ثانویه مورد انتظار تصمیم گیری می‌کنیم
تئوری بیز در یادگیری ماشین
در یادگیری ماشین معمولاً در فضای فرضیه H بدنبال بهترین فرضیه‌ای هستیم که درمورد داده‌های آموزشی D صدق کند. یک راه تعیین بهترین فرضیه، این است که بدنبال محتمل ترین فرضیه‌ای باشیم که با داشتن داده‌های آموزشی D و احتمال قبلی در مورد فرضیه‌های مختلف می‌توان انتظار داشت تئوری بیز چنین راه حلی را ارائه می‌دهد. این روش راه حل مستقیمی است که نیازی به جستجو ندارد.
سنگ بنای یادگیری بیزی را تئوری بیز تشکیل می‌دهد. این تئوری امکان محاسبه احتمال ثانویه را بر مبنای احتمالات اولیه می‌دهد:
همانطور که مشاهده می‌شود با افزایش 
مقدار 
کاهش می‌یابد. زیرا هر چه احتمال مشاهده D مستقل از h بیشتر باشد به این معنا خواهد بود که D شواهد کمتری در حمایت از hدر بر دارد.
تعریف مفاهیم اولیه
فرض کنید که فضای فرضیه 
و مجموعه مثالهای آموزش 
موجود باشند. مقادیر احتمال زیر را تعریف می‌کنیم:
: احتمال اولیه‌ای (prior probablity) که فرضیه h قبل از مشاهده مثال آموزشی داشته‌است . اگر چنین احتمالی موجود نباشد می‌توان به تمامی فرضیه‌ها احتمال یکسانی نسبت داد.- :احتمال اولیه‌ای که داده آموزشی مشاهده خواهد شد.
:احتمال مشاهده داده آموزشی به فرض آنکه فرضیه صادق باشد.- :احتمال ثانویه (posterior probablity) نامیده می‌شود یعنی احتمال اینکه با مشاهده داده آموزشی فرضیه صادق باشد و
در یادگیری ماشین به دنبال یافتن این احتمال است.
توجه شود که احتمال اولیه () مستقل از داده آموزشی است ولی احتمال ثانویه () تاثیر داده آموزشی را منعکس می‌کند.
روشهای یادگیری بیزی ماشینی
روشهای بیزی فرضیه‌هائی ارائه می‌دهند که قادر به پیش بینی احتمالی هستند (مثل بیمار به احتمال ۹۳% بهبود می‌یابد) مثالهای جدید را می‌توان با ترکیب وزنی چندین فرضیه دسته بندی نمود. حتی در مواردی که روشهای بیزی قابل محاسبه نباشند، می‌توان از آنها به عنوان معیاری برای ارزیابی روشهای دیگر استفاده کرد تعدادی از روشهای یادگیری ماشینی بیزی شامل موارد زیر است:
- Bayes Optimal Classifier
- دسته‌بندی کننده نایو بیز
- شبکه‌های بیزی
قضیه بیز
از ویکی‌پدیا، دانشنامهٔ آزادقضیه بیز (به انگلیسی: Bayes’ theorem) روشی برای دسته بندی پدیده‌ها، بر پایه احتمال وقوع یا عدم وقوع یک پدیده‌است و در نظریه احتمالات با اهمیت و پرکاربرد است. اگر برای فضای نمونه‌ای مفروضی بتوانیم چنان افرازی انتخاب کنیم که با دانستن اینکه کدامیک از پیشامدهای افراز شده رخ داده‌است، بخش مهمی از عدم‌اطمینان تقلیل می یابد.
این قضیه از آن جهت مفید است که می‌توان از طریق آن احتمال یک پیشامد را با مشروط کردن نسبت به وقوع و یا عدم وقوع یک پیشامد دیگر محاسبه کرد. در بسیاری از حالت‌ها، محاسبهٔ احتمال یک پیشامد به صورت مستقیم کاری دشوار است. با استفاده از این قضیه و مشروط کردن پیشامد مورد نظر نسبت به پیشامد دیگر، می‌توان احتمال مورد نظر را محاسبه کرد.
این رابطه به خاطر بزرگداشت توماس بیز فیلسوف انگلیسی به نام فرمول بیز معروف است.
معادله اصلی
فرض می‌کنیم
یک افراز برای فضای نمونه‌ای تشکیل دهند. طوری که به ازای هر ، داشته باشیم و فرض کنید پیشامدی با فرض باشد، در اینصورت به ازای ، داریم:
یادگیری ماشینی به کمک نظریه بیز
برای نگرش بیزی به یادگیری ماشین (و یا هر فرایند دیگر) می‌باید نخست:
- دانش موجود در باره موضوع را بصورت احتمالاتی فرموله کنیم:برای اینکار باید مقادیر کیفی دانش را بصورت توزیع احتمال، فرضیات استقلال و غیره مدل کرد. این مدل دارای پارامترهای ناشناخته‌ای خواهد بود که برای هر یک از مقادیر ناشناخته، توزیع احتمال اولیه‌ای در نظر گرفته می‌شود که بازگو کننده باور ما به محتمل بودن هر یک ازاین مقادیر بدون دیدن داده‌است.
- با جمع آوری داده و مشاهدهٔ آن، مقدار توزیع احتمال ثانویه را محاسبه می‌کنیم
- با استفاده از این احتمال ثانویه:
- به یک نتیجه گیری در مورد عدم قطعیت می‌رسیم
- با میانگین گیری روی مقادیر احتمال ثانویه پیش بینی انجام می‌دهیم
- برای کاهش خطای ثانویه مورد انتظار تصمیم گیری می‌کنیم
تئوری بیز در یادگیری ماشین
در یادگیری ماشین معمولاً در فضای فرضیه H بدنبال بهترین فرضیه‌ای هستیم که درمورد داده‌های آموزشی D صدق کند. یک راه تعیین بهترین فرضیه، این است که بدنبال محتمل ترین فرضیه‌ای باشیم که با داشتن داده‌های آموزشی D و احتمال قبلی در مورد فرضیه‌های مختلف می‌توان انتظار داشت تئوری بیز چنین راه حلی را ارائه می‌دهد. این روش راه حل مستقیمی است که نیازی به جستجو ندارد.
سنگ بنای یادگیری بیزی را تئوری بیز تشکیل می‌دهد. این تئوری امکان محاسبه احتمال ثانویه را بر مبنای احتمالات اولیه می‌دهد:
همانطور که مشاهده می‌شود با افزایش
مقدار کاهش می‌یابد. زیرا هر چه احتمال مشاهده D مستقل از h بیشتر باشد به این معنا خواهد بود که D شواهد کمتری در حمایت از hدر بر دارد.تعریف مفاهیم اولیه
فرض کنید که فضای فرضیه
و مجموعه مثالهای آموزش موجود باشند. مقادیر احتمال زیر را تعریف می‌کنیم:- : احتمال اولیه‌ای (prior probablity) که فرضیه h قبل از مشاهده مثال آموزشی داشته‌است . اگر چنین احتمالی موجود نباشد می‌توان به تمامی فرضیه‌ها احتمال یکسانی نسبت داد.
- :احتمال اولیه‌ای که داده آموزشی مشاهده خواهد شد.
- :احتمال مشاهده داده آموزشی به فرض آنکه فرضیه صادق باشد.
- :احتمال ثانویه (posterior probablity) نامیده می‌شود یعنی احتمال اینکه با مشاهده داده آموزشی فرضیه صادق باشد و
در یادگیری ماشین به دنبال یافتن این احتمال است.
توجه شود که احتمال اولیه (
) مستقل از داده آموزشی است ولی احتمال ثانویه () تاثیر داده آموزشی را منعکس می‌کند.روشهای یادگیری بیزی ماشینی
روشهای بیزی فرضیه‌هائی ارائه می‌دهند که قادر به پیش بینی احتمالی هستند (مثل بیمار به احتمال ۹۳% بهبود می‌یابد) مثالهای جدید را می‌توان با ترکیب وزنی چندین فرضیه دسته بندی نمود. حتی در مواردی که روشهای بیزی قابل محاسبه نباشند، می‌توان از آنها به عنوان معیاری برای ارزیابی روشهای دیگر استفاده کرد تعدادی از روشهای یادگیری ماشینی بیزی شامل موارد زیر است:
- Bayes Optimal Classifier
- دسته‌بندی کننده نایو بیز
- شبکه‌های بیزی